Az előző posztban megnéztük hogyan definiálja a GDPR a személyes adat fogalmát és mi számít személyes adatnak a definíció szerint.
Ebben a posztban egy mérnöki (és talán jogi) szempontból jóval izgalmasabb kérdést vizsgálunk: Személyes adatnak minősülhet-e az aggregált/statisztikai adat?
A probléma azért érdekes, mert a legtöbb cég/kormány/szervezet többnyire aggregált adatokat oszt meg, bízva abban, hogy ezek nem személyes adatok. Valóban, a GDPR így nyilatkozik a statisztikai adatról (26. preambulum): “[…] Az adatvédelem elveit […] az anonim információkra nem kell alkalmazni, nevezetesen olyan információkra, amelyek nem azonosított vagy azonosítható természetes személyre vonatkoznak, valamint az olyan személyes adatokra, amelyeket olyan módon anonimizáltak, amelynek következtében az érintett nem vagy többé nem azonosítható. Ez a rendelet ezért nem vonatkozik az ilyen anonim információk kezelésére, a statisztikai vagy kutatási célú adatkezelést is ideértve.”
Később (162. preambulum):
“[…] Statisztikai célúnak minősül a személyes adatok statisztikai felmérések vagy statisztikai eredmények kiszámításának céljából történő gyűjtése és kezelése. […] A statisztikai célból következik, hogy a statisztikai célú adatkezelés eredménye nem személyes adat, hanem összesített [aggregált] adat, és hogy ezt az eredményt vagy a személyes adatokat nem használják fel konkrét természetes személyekre vonatkozó intézkedések vagy döntések alátámasztására.”
Mindazonáltal a GDPR is elismeri a 89. cikkben, hogy a statisztikai adatok nem feltétlenül anonim adatok, és azokra az adatvédelmi szabályozás már alkalmazandó.
Ebben a posztban megmutatjuk, hogy aggregált adatokból valóban rekonstruálhatók személyes adatok (pontosabban egyének rekordjai egy adatbázisban amin az aggregált adatot számolták), és így aggregált (összesített) adat is lehet személyes adat, akár még a GDPR 4. cikkének értelmezésében is. Példaként azt is megmutatjuk, hogy ha egy telekom cég kiadná a mobiltelefon-tornyok látogatottságát az idő függvényében (vagyis minden egyes toronynál levő előfizetők számát fél óránként), akkor ebből az aggregált adatból az egyes előfizetők által meglátogatott tornyok (helyek) listája közel 80%-os pontossággal rekonstruálható. Így az ilyen összesített adat lehet személyes (sőt akár érzékeny), és ebben az esetben az ilyen adat megfelelő anonimizációja/torzítása lehet szükséges.
Mi az aggregált adat?
A GDPR ugyan nem definiálja az aggregált (összesített) adat fogalmát, de valószínűleg több egyén adatán számolt statisztikai/összesített adatot ért alatta. Például az 1. táblázatban aggregált adat a betegek vércukrának átlaga, vagy szórása, vagy eloszlása, stb. Valójában az aggregált/statisztikai adatok előállíthatók több elemi ún. számláló lekérdezések (counting query) eredményeinek valamilyen függvényeként. Ilyen lekérdezés például: Hány olyan beteg van az adatbázisban akik Alzheimerben szenvednek? Vagy, hány olyan beteg van akiknek a vércukra 4.1 és 4.2 közé esik? Az ilyen lekérdezéseket egy mintával definiáljuk (pl. betegség attribútum értéke “Alzheimer”, vagy vércukor attribútum értéke egy adott tartományba esik), és eredményük azon rekordok száma az adatbázisban, amelyekre az adott minta illeszkedik (úgy mondjuk, hogy az ilyen rekordokat a lekérdezés lefedi). Például az 1. táblázaton alkalmazva az első lekérdezés eredménye 1, mivel csak egy beteg szenved Alzheimerben (vagyis ez a lekérdezés csak a 3. rekordot fedi le). A második lekérdezés eredménye viszont 0, mivel egy beteg vércukra sem esik 4.1 és 4.2 közé.
A számláló lekérdezésekkel szinte az összes statisztikai adat kiszámolható.
Például ha kiváncsiak vagyunk betegségek eloszlására/hisztogramjára az adatbázisban (vagyis az egyes betegségek gyakoriságára), akkor minden betegség előfordulását meg kell számolni az adatbázisban (annyi lekérdezés szükséges ahány betegség lehetséges). Építhetők finomabb eloszlások specifikusabb mintával; pl. Hány olyan beteg van az adatbázisban akik Alzheimerben szenvednek és 40 évnél fiatalabb és Budapesten laknak? Numerikus attribútumra (pl. vércukor) hasonló az eljárás, de ott a minta értéktartományokat tartalmaz (pl. hány olyan beteg van akiknek a vércukra 4.1 és 4.2 közé esik?).
Az ilyen eloszlásokból pedig további statisztikák számolhatók; átlagok, szórások, medián, max, min, stb.
| Rekord | Nem | Irányítószám | Vércukor | Betegség |
|---|---|---|---|---|
| 1. | Kovács Attila | 1123 | 4.3 | Meningitis |
| 2. | Kovács Attila | 1123 | 5.2 | Crohn-betegség |
| 3. | Kovács Ferenc | 1114 | 6.1 | Alzheimer |
| 4. | Kovács Ferenc | 8423 | 3.2 | Crohn-betegség |
| 5. | Kovács Ferenc | 1114 | 7.1 | Lábfejtörés |
| 6. | Nagy Tibor | 1113 | 6.2 | Crohn-betegség |
1. táblázat: Kórházi adatok
A számláló lekérdezések univerzitása miatt általában elég ha csak a számláló lekérdezések eredményeit osztják meg (mint aggregált adatot), amit aztán további statisztikai adatok számításához felhasználhatnak a kérdezők. Ezért a továbbiakban csak ilyen lekérdezésekre fókuszálunk, és aggregált (statisztikai) adat alatt számláló lekérdezések eredményeinek összességét értjük.
FONTOS: A vizsgálat célja csakis az aggregált adat, nem az adatbázis amin az aggregátumot számoljuk. Más szavakkal a kérdés, hogy személyes adatnak minősülhetnek-e az aggregátumok (bizonyos mintára illeszkedő rekordok száma) egy olyan támadó számára, aki nem fér hozzá az adatbázishoz?
Interaktív és nem interaktív lekérdezések
Van amikor a cég megengedi, hogy a kérdezők (támadók) specifikálják a lekérdezéseket a korábbi lekérdezéseik függvényében (interaktív, online eset), de van amikor csak előre meghatározott lekérdezések eredményeit teszik közzé (nem interaktív, offline eset). Nyilván az interaktív eset veszélyesebb adatvédelmi szempontból, hiszen akkor a támadó a lekérdezéseit a korábbi lekérdezések eredményeinek a függvényében állíthatja össze (adaptív támadás).
Célzott támadás
Tekintsük Zsuzsa nénit az előző posztból, aki a Facebookon talál egy K. Ferenc nevű felhasználót. K. Ferenc megosztott képei alapján egy kis községben lakik, aminek az irányítószámát is megadta (8423), a 20-as éveiben jár, és krónikus bőrkiütésben szenved (a pontos betegségét ez alapján még nem ismeri). Zsuzsa néni ugyan az 1. táblázathoz nem fér hozzá, de jogosult az alábbi lekérdezéshez: Hány olyan beteg van aki az X irányítószám alatt lakik és a betegsége Y? Ezután lefuttatja az összes olyan kérést, ahol X=8423 és Y pedig egy olyan betegség, aminek tünete a krónikus bőrkiütés. Ha csak egy ilyen lekérdezés értéke 1 a többié pedig 0, akkor Zsuzsa néni megtalálta K. Ferenc pontos betegségét (erre jó esély van ha K. Ferenc vidéki, és a községben ahol él más nem volt a kórházban krónikus bőrkiütéssel).
Ismét látható, hogy a támadó háttértudása (a publikus információ, hogy egy fiatal K. Ferenc krónikus bőrkiütésben szenved és egy ismert községben lakik) lehetővé teheti személyes adatok visszafejtését aggregált adatokból. Ahogyan azt az előző posztban is megmutattuk, manapság a legtöbb emberről rengeteg nyilvános adat elérhető maguk vagy mások által, így a hasonló támadások létezését lehetetlen kizárni. Például előfordulhat, hogy Zsuzsa néni nemcsak bőrkiütést hanem egyéb más tünetet is megfigyel K. Ferencről a képei alapján, így a szóba jöhető betegségek száma kevesebb, vagyis még kevesebb lekérdezésből még nagyobb eséllyel kiderítheti K. Ferenc pontos betegségét.
Például videón szereplő személyek pulzusa megállapítható pusztán a videóból az illetők tudta nélkül.
Naívan gondolhatnánk, hogy az ilyen támadások megelőzhetők ha nem válaszolunk meg olyan lekérdezéseket, amelyek eredménye túl kicsi (vagyis túl kevés rekordot fednek le). Sajnos ez nem mindig segít; pl. az 1. táblázatban az összes Crohn betegek száma 3 (első lekérdezés), a budapesti Crohn betegek száma 2 (második lekérdezés), akkor a kettő különbsége adja a vidéki Crohn betegek számát amire csak egy rekord illeszkedik (K. Ferenc), és amit így már nem kell lekérdezni (differencing attack). Az ilyen “problémás” lekérdezések detekciója nem mindig könnyű,
mivel általános esetben két lekérdezés ekvivalenciája eldönthetetlen, valamint az egyes rekordok kiszámíthatóságának eldöntése adott aggregátumokból gyakran nehéz probléma.
A következőkben több személyt érintő globális (mass) támadásokra fókuszálunk, és a fenti differencing támadás ötletét általánosítjuk; megmutatjuk, hogy ha elég sok lekérdezést válaszolnak meg, akkor egy támadó képes lehet az eredeti rekordokat visszaállítani a lekérdezések összességéből függetlenül az egyes eredmények nagyságától.
Először ezt egy olyan példán mutatjuk be, ahol a támadó a lekérdezéseket ő maga választja. Látni fogjuk, hogy kb. a rekordok számával megegyező lekérdezésekből a rekordok jó része helyreállítható. A második példában a támadó nem interaktív, vagyis nem képes a lekérdezéseket megválasztani, de így is rekonstruálhatja a rekordok több mint 70%-át az adat jellemzőit (mint háttértudást) kihasználva.
Globális támadás 1: Rekordok interaktív helyreállítása
A támadás alapötlete, hogy minden egyes megválaszolt lekérdezéssel növeljük egy sikeres differencing támadás esélyét valamely rekordra.
Kicsit pontosabban, minden megválaszolt lekérdezés egy egyenletet definiál a lefedett rekordokon mint ismeretleneken. Ha elég sok egyenletünk (megválaszolt lekérdezésünk) van, akkor azok egyértelműen megoldhatóvá válnak és az ismeretlenek (rekordok) meghatározhatók.
Vegyük példaként a 2. és 3. táblázatot, ahol a 2. táblázat a 3. táblázatban szereplő egyének kvázi azonosítóit tartalmazza. A 3. táblázat
első attribútuma az illető korának felel meg (ugyanaz mint a 2. táblázat 3. oszlopa), a többi attribútumok pedig Budapest főbb helyeit (POI) reprezentálják, és értékük 1, ha az illető meglátogatta az adott helyet, egyébként nulla. Tegyük fel, hogy a két táblázat rekordjai ugyanahhoz a személyhez tartoznak (vagyis a 3. táblázat i-ik sora és 4. táblázat i-ik sora ugyanazon személy adatai).
| Rekord | Nem | Kor | Lakhely |
|---|---|---|---|
| 1. | Férfi | 23 | Budapest |
| 2. | Nő | 43 | Budapest |
| 3. | Férfi | 45 | Budapest |
| 4. | Nő | 36 | Budapest |
| … | … | … | … |
2. táblázat: Demográfiai adatok (kvázi azonosítók)
A 2. táblázathoz hozzáfér a támadó, viszont a 3. táblázathoz nem. Tegyük fel továbbá, hogy a támadó az alábbi Q([X,Y],Z) lekérdezést hajthatja végre: Hány olyan személy van a 3. táblázatban, akiknek kora az [X, Y] intervallumba esik és meglátogatták a Z helyet?
Vagyis Q([X,Y], Z) azon rekordok számát jelöli, ahol a kor értéke legalább X és legfeljebb Y, valamint Z attribútum/hely értéke 1. Tegyük fel, hogy nem válaszolunk meg túl kevés rekordot lefedő lekérdezéseket (pl. ha Q([X,Y],Z)<10), az adatbázisban pedig több száz rekord van.
A támadó célja a 3. táblázat rekonstruálása a lekérdezések eredményeit és a 2. táblázatot felhasználva.
| Rekord | Kor | Móricz Zsigmond körtér | Allee | Mom Park | … | Széll Kálmán tér |
|---|---|---|---|---|---|---|
| 1. | 23 | 0 | 1 | 1 | … | 0 |
| 2. | 43 | 1 | 1 | 1 | … | 0 |
| 3. | 45 | 0 | 0 | 0 | … | 1 |
| 4. | 36 | 0 | 0 | 1 | … | 1 |
| … | … | … | … | … | … |
3. táblázat: Helyzeti adatok
Először csak egy oszlopot rekonstruálunk, a többi hasonlóan történik. Legyen Z egy előre kiválasztott hely (pl. Z = “Allee”). A cél a 3. táblázat Z értékének megfelelő oszlopának rekonstruálása, amit x_1, x_2, \ldots, x_n ismeretlenekkel jelölünk és ahol n az összes rekordok száma a táblázatban (vagyis x_i=1 ha a támadó szerint az i-ik rekord meglátogatta a Z helyet, egyébként x_i=0). A támadás lényegében egy egyszerű lineáris egyenletrendszer megoldásából áll:
- Válaszd a kor lehetséges értékeinek egy véletlen intervallumát (pl. [X=32;Y=40])?
- Kérdezd a Q([X,Y],Z) értékét
- Ismételd meg a fenti műveleteket t-szer, így kapod t darab lekérdezés eredményeit: Q_1([X_1, Y_1], Z), Q_2([X_2, Y_2], Z), \ldots, Q_t([X_t, Y_t], Z)
- Minden Q_j lekérdezéshez határozd meg azon S_j \subseteq \{1,2, \ldots, n\} rekordok halmazát a 2. táblázatból, amelyet a Q_j lekérdezés lefed (vagyis a koruk a [X_j, Y_j] intervallumba esik).
- Old meg az alábbi t egyenletből és n feltételből álló lineáris egyenletrendszert:
\begin{matrix}
\sum_{i \in S_1} x_i = Q_1([X_1, Y_1], Z),\\
\sum_{i \in S_2} x_i = Q_2([X_2, Y_2], Z), \\
\vdots\\
\sum_{i \in S_t} x_i = Q_t([X_t, Y_t], Z),
\end{matrix}
\text{ahol:}\; 0 \leq x_i \leq 1 -
Kerekítsd x_i értékeit: x_i = 1 ha x_i > 1/2, máskülönben x_i = 0
Bebizonyítható, hogy $t= n \log^2 n$ megválaszolt lekérdezés esetén a 6. lépésben kapott $x_i$ értékek nagy része helyes (tehát x_1, x_2, \ldots, x_n megegyezik a 3. táblázat Z értének megfelelő oszlopával), és így az eredeti adatbázis Z értékének megfelelő oszlopa rekonstruálható. Pl. ha az adatbázisban 128 rekord van, akkor abból legalább 124 helyreállítható így.
Természetesen a 3. táblázat egy visszaállított oszlopa önmagában még nem minősül személyes adatnak, hiszen ahhoz minden visszaállított értékhez hozzá kellene rendelni egy természetes személyt. Ezért a fenti támadás megismételhető több, mondjuk k>20 oszlopra/helyre.
Ha valaki szerepel az adatbázisban, akkor annak 5-10 helye már egyértelműen azonosítja azt, ezért az illető publikusan elérhető Facebook/Instagram profilja összevethető a rekonstruált rekordokkal; jó eséllyel csak az ő rekonstruált rekordja fogja a Facebook profiljában szereplő helyek együttesét tartalmazni.
Mivel a rekonstrukciós pontosság magas, a támadás sikervalószínűsége elég nagy. Így ha a támadás plauzibilis (a támadó valóban hozzáfér a 2. táblázathoz és a személyek közösségi profiljához), akkor a lekérdezések összessége személyes adatnak minősülhet a GDPR szerint.
Megjegyzések:
- A 4. lépésben megoldandó egyenletrendszer azért lineáris, mert a lekérdezések (subset-sum query) az attribútum-értékek lineáris függvénye (jelen esetben összege). Az egyenletrendszer bármely LP solver-rel megoldható (pl. CPLEX, glpk, stb.).
- Az eredeti adatbázis visszaállíthatósága t= n \log^2 n lekérdezés esetén garantált, ahol minden lekérdezés minden rekordot 1/2 eséllyel tartalmaz. Ez a fenti példában nem feltétlen igaz, hiszen ott a kor alapján választunk egyenletes eloszlás szerint nem pedig magukat a rekordokat 1/2 valószínűséggel (ebből az is következik, hogy a fenti támadás nem adaptív). Ennek ellenére a gyakorlatban a támadás jó eséllyel működik.
- A megoldandó egyenletrendszer n változót és t= n \log^2 n egyenletet/feltételt tartalmaz. Létezik olyan támadás, ami t= n lekérdezéssel hasonló rekonstrukciós pontosságot ér el, viszont itt a lekérdezéseket determinisztikusan és nem véletlenszerűen választják.
- Ezek a támadások akkor is működhetnek, ha a lekérdezések értékéhez véletlen zajt adunk hozzá (query perturbation). Ebben az esetben egyenletek helyett egyenlőtlenségek rendszerét kell megoldani, aminek megoldása az első támadással a legrosszabb esetben O(n^5 \log^4 n) lépést, míg a másodikkal csak O(n\log n) lépést igényel. Ha a zaj által okozott abszolút hiba legfeljebb E, akkor n – 4E^2 rekord helyreállítható. Pl. ha n=256 és E=3, akkor 220 rekord helyreállítható. Viszont érdekes módon $E > \sqrt{n}$ torzítás már megakadályozhatja a rekordok rekonstrukcióját.
Globális támadás 2: Telekom (CDR) adatok nem interaktív helyreállítása
A fenti támadás azért működik, mert a támadó a lekérdezéseket (pontosabban azok mintáját) képes megválasztani. Ebben az is segíti, hogy hozzáfér minden rekord kvázi azonosítóihoz (2. táblázathoz), és így pontosan tudja, hogy melyik lekérdezés melyik rekordokat fedi le. Ha ezt nem tudná, akkor az 5. lépésben definiált egyenletrendszer nem lenne megoldható, hiszen nem tudná, hogy pontosan melyik ismeretlenek (rekordok) szerepelnek az egyenletek bal oldalán. Felmerül a kérdés: sikeres lehet-e egy olyan nem interaktív támadás, ahol a lekérdezéseket a támadó nem tudja megválasztani, a rekordok többségének kvázi azonosítóit nem ismeri, és csak előre definiált lekérdezések eredményét ismerheti? Ez egy gyengébb támadó jóval kevesebb háttértudással, és így sokkal inkább plauzibilis a gyakorlatban. Ha egy ilyen plauzibilis támadó sikervalószínűsége elég nagy, akkor gyanítható, hogy az aggregált adat személyesnek minősül még a GDPR 4. cikkének értelmében is.
Ezt megerősítve a következőkben bemutatunk egy közelmúltban publikált támadást egy gyakorlati alkalmazáson a fenti plauzibilis támadót feltételezve.
Az adat
Napjainkban népszerű statisztikai adat az emberek térbeli sűrűsége, vagyis bizonyos helyek (POI-k) látogatottsága az idő függvényében. Ez az aggregált adat értékes, hiszen felhasználható közlekedési hálózat optimalizációjára, új szolgáltatások (pl. áruházak) telepítési helyének meghatározásához, de akár járványok terjedésének modellezéséhez is.
Egy populáció ilyen térbeli eloszlása jól becsülhető a használatban levő mobiltelefonok helyzeti információiból; amikor egy előfizető hívást vagy adatforgalmat kezdeményez/fogad, rögzítésre kerül a telefontorony (és az időpont), amellyel az előfizető telefonja kapcsolatban van. Mivel az ilyen tornyok elég sűrűn helyezkednek el (főleg sűrűn lakott területen), így a tornyok pozíciójából az előfizetők térbeli helyzete jól becsülhető.
Ezt felismerve sok telekom cég monetizálná az ilyen hívási (ún. CDR) meta-adatokat. Viszont, ahogy az előző posztban is utaltunk rá, egy ilyen adatbázis nagy valószínűséggel sok személyes adatot tartalmaz, hiszen egy előfizető 4-5 tornya már jó eséllyel egyedi azonosítónak számít. Ezért a telekom cégek többsége a CDR adatot nem osztja meg, hanem csak az abból számolt aggregátumokat; minden toronyhoz az ott tartózkodott előfizetők számát minden fél órában (vagyis minden toronyhoz egy idősort). A következőkben megmutatjuk, hogy az ilyen statisztikai adat is lehet személyes.
A támadás célja
Adott n előfizető akiknek hívási adataikat rögzítik m toronynál az eredeti CDR adatbázisban. Az egyes tornyokat jelölje T_1, T_2, \ldots, T_m. Ebből az adatbázisból a cég minden t időpontban kiszámolja a \mathbf{P}^t = (p_1^t, p_2^t, \ldots, p_m^t) torony-látogatottságokat, ahol p_j^t jelöli az T_j toronynál levő előfizetők számát a t-edik időintervallumban/időpontban (pl. egy fél óra alatt). A cég csakis a \mathbf{P}^t-t osztja meg másokkal, bízva abban, hogy az ilyen aggregált adat nem minősül személyes adatnak.
Legyen Y_{i,j}^t = 1, ha az i-edik előfizető meglátogatta T_j tornyot a t időtartományban, máskülönben 0. Így \mathbf{Y}^t egy n \times m méretű bináris mátrix ami az egyes előfizetők toronylátogatásait reprezentálja t időpontban. A támadás célja az Y_{i,j}^t értékek rekonstruálása minden i előfizetőre, T_j toronyra, és t időpontra úgy, hogy (1) \sum_{i=1}^n Y_{i,j}^t = p_{j}^t, vagyis az \mathbf{Y}^t mátrix j oszlopában található elemek összege a T_j tornyot meglátogatott előfizetők száma egy időpontban, valamint (2) \sum_{j=1}^m Y_{i,j}^t = 1, vagyis egy előfizető egy időpontban (itt fél órában) csak egy tornyot látogathat meg. Ha többet látogat meg, akkor vesszük a legtöbbet meglátogatott tornyot az adott fél órában. Mivel vannak előfizetők akik nem minden fél órában használják a telefonjukat, az ilyen fél órákban a feltételezett toronylátogatásokat interpolációval becsüljük az ismert toronylátogatásokból.
A támadás alapötlete és menete
Ugyan a támadás első hallásra meghökkentő, az adat jellegét megnézve már nem tűnik olyan hihetetlennek. Valójában az adat három fő tulajdonságát használják ki:
- Predikálhatóság: Minden előfizető tornya egy adott időpontban jól becsülhető a korábban meglátogatott tornyokból; az időben következő torony szinte mindig közel van földrajzilag az éppen meglátogatott toronyhoz. Ezt azt is jelenti, hogy az előfizetők (ill. rekordjaik) jól szeparálhatók, hiszen ha két rekord t időpontban távol van egymástól, azok jó eséllyel a (t+1)-ben is távol lesznek egymástól.
-
Regularitás: Az előfizetők többsége minden nap hasonló (gyakran ugyanazon) tornyokat látogatja meg hasonló időkben, mivel a legtöbb ember napi rutinjai azonosak.
-
Egyediség: Az előfizetők egymástól elég különböző tornyokat látogatnak meg, amit már több tanulmány szemléltetett; egy több milliós populációban egy előfizető bármely 4 meglátogatott tornya (az időpont órás pontosságával) egyedivé teszi őt az előfizetők között az esetek 98%-ában.
A három tulajdonságot szemlélteti az alábbi ábra, ahol 5 különböző előfizető térbeli helyzete látható két egymást követő nap.
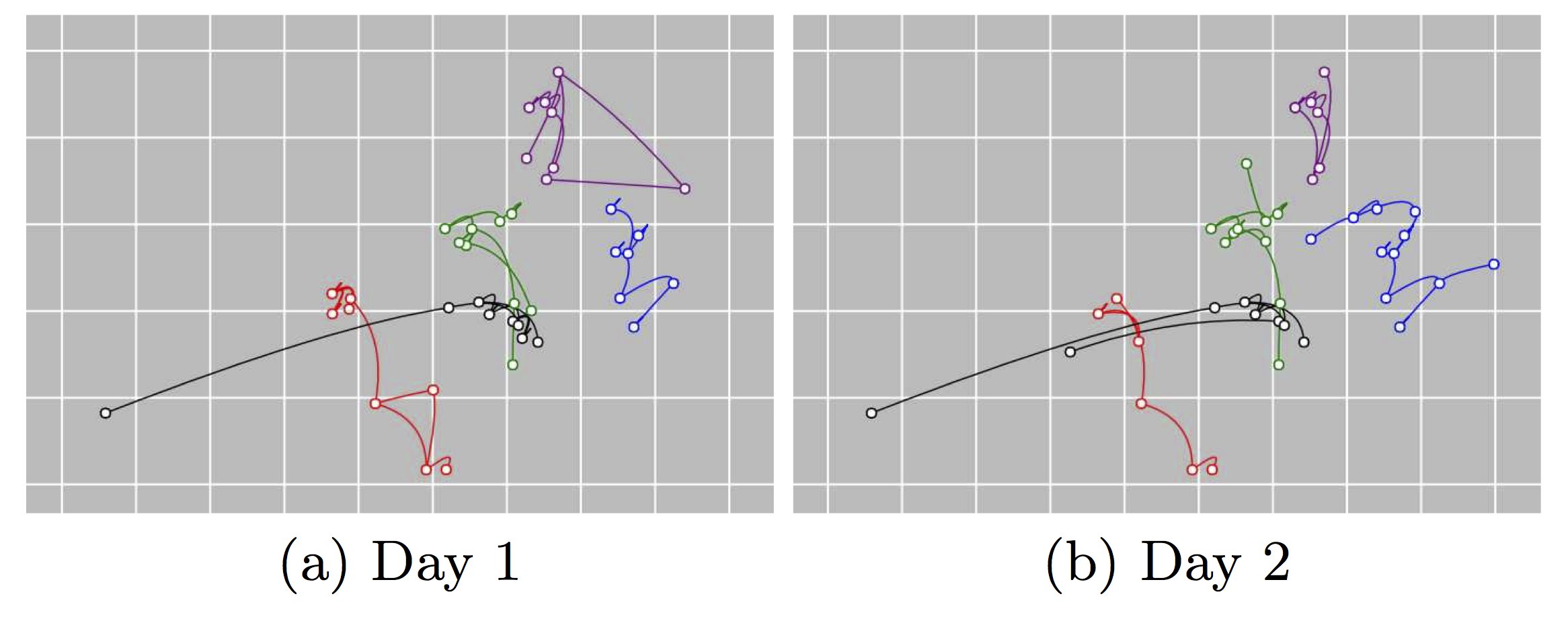
A támadás először a rekordok predikálhatóságát felhasználva rekonstruálja a rekordokat (azaz az \mathbf{Y}^t mátrixot) minden t-re egy napon belül, feltéve, hogy \mathbf{P}^t ismert.
Ezt megismétli minden egyes napra külön-külön. Végül a rekordok regularitását és egyediségét felhasználva az azonos előfizetőhöz tartozó rekonstruált rekordokat összerendeli a napok között.
Rekordok rekonstruálása adott t időpontban
Tegyük fel, hogy a (t-1)-beli toronylátogatások ismertek \mathbf{Y}^{t-1} formájában, valamint az összes torony látogatottsága t-ben \mathbf{P}^t formájában. Hogyan tudnánk ezekből rekonstruálni \mathbf{Y}^{t}-t?
Ha egy előfizető a (t-1)-ben a T_j tornyot látogatta meg, akkor jó eséllyel a t időpontban a T_j toronyhoz közelebbi tornyokat fogja meglátogatni, vagyis lesznek tornyok amiket nagyobb eséllyel látogat meg, és lesznek amiket kisebb eséllyel a korábban meglátogatott tornyok (pl. T_j) függvényében. Így minden előfizető-torony (i,j) párhoz hozzá tudunk rendelni egy c_{i,j}^t “költséget” az idő függvényében, aminek értéke nagyobb, ha az i előfizető kisebb eséllyel látogatta meg a T_j tornyot, és kisebb, ha nagyobb eséllyel látogatta azt meg a t időpontban. Keressük azt az előfizetők és tornyok közötti összerendelést t időpontban (vagyis \mathbf{Y}^{t}-t), ami az összes előfizetőhöz az általuk legnagyobb eséllyel meglátogatott tornyokat rendeli.
Lényegében az alábbi optimalizációs problémát kell megoldanunk minden t időpontban, ahol az ismeretlenek \mathbf{Y}^{t} mátrix elemei:
\begin{matrix}
\text{Adott}\; P^t = (p_1^t, p_2^t, \ldots, p_m^t), \\
\text{minimalizáld}\; \sum_{i=1}^n \sum_{j=1}^m c_{i,j}^t \times Y_{i,j}^t\; \text{összeget,}\\
\text{feltéve, hogy }\; Y_{i,j}^t \in \{0,1\},\: \sum_{i=1}^n Y_{i,j}^t = p_{j}^t,\: \sum_{j=1}^m Y_{i,j}^t = 1
\end{matrix}
A feladatot elképzelhetjük mint az alábbi gráf probléma megoldását minden t időpontban. A gráf bal oldalán vannak az előfizetőknek megfelelő csúcsok, a jobb oldalon pedig a tornyoknak megfelelő csúcsok. Élek csakis a két oldal között lehetnek, ahol minden él súlya megegyezik az adott előfizető-torony pár költségével.
Egy i előfizető és j torony között akkor van él, ha az i előfizető meglátogatta j tornyot a t időpontban.
A feladat a bal és jobb oldali csúcsok összekötése úgy, hogy (1) minden jobb oldalon levő csúcshoz (toronyhoz) csakis annyi bal odalon levő csúcsot (előfizetőt) köthetünk, ahányan meglátogatták azt a tornyot t időpontban (ez adott \mathbf{P}^t által), (2) egy bal oldali csúcshoz (előfizetőhöz) csakis egy jobb oldali csúcs (torony) rendelhető, mivel egy előfizető bármely időpontban csak egyetlen tornyot látogathat meg, (3)
az összes így kapott él súlyának összege (összköltség) minimális legyen (vagyis keressük a globálisan legvalószínűbb toronylátogatásokat). Ez egy összerendelési probléma (assigment problem) ami hatékonyan megoldható a magyar módszerrel, viszont ehhez a gráf minimális átalakítása szükséges.
Egész pontosan a magyar algoritmus olyan esetekben működik, ahol egy bal oldali csúcshoz csakis egy jobb oldali csúcs tartozhat, és egy jobb oldalihoz csakis egy bal oldali. Az így kapott súlyozott teljes páros gráfon képes az eljárás minimális/maximális összsúlyú teljes párosítást keresni. Ez könnyen elérhető a mi esetünkben, ha minden tornyot annyi csúccsal reprezentálunk, ahányan meglátogatták azt a t időpontban, valamint egy adott előfizetőt egy torony “replikált” csúcsaihoz azonos költséggel rendelünk (más szavakkal egy i előfizetőt a T_j toronyhoz tartozó csúcs bármelyikéhez csakis c_{i,j}^t súlyú éllel köthetünk). Ebből következik, hogy az átalakított gráf bal és jobb oldalán levő csúcsok száma megegyezik. A két gráf közötti különbséget szemlélteti az alábbi ábra, ahol p_1^t=2 és p_2^t=1 (vagyis az első tornyot ketten látogatták meg t-ben, ezért azt két darab csúccsal reprezentáljuk az átalakított gráfban, míg a másodikat csak eggyel).
| Eredeti gráf | Átalakított gráf |
|---|---|
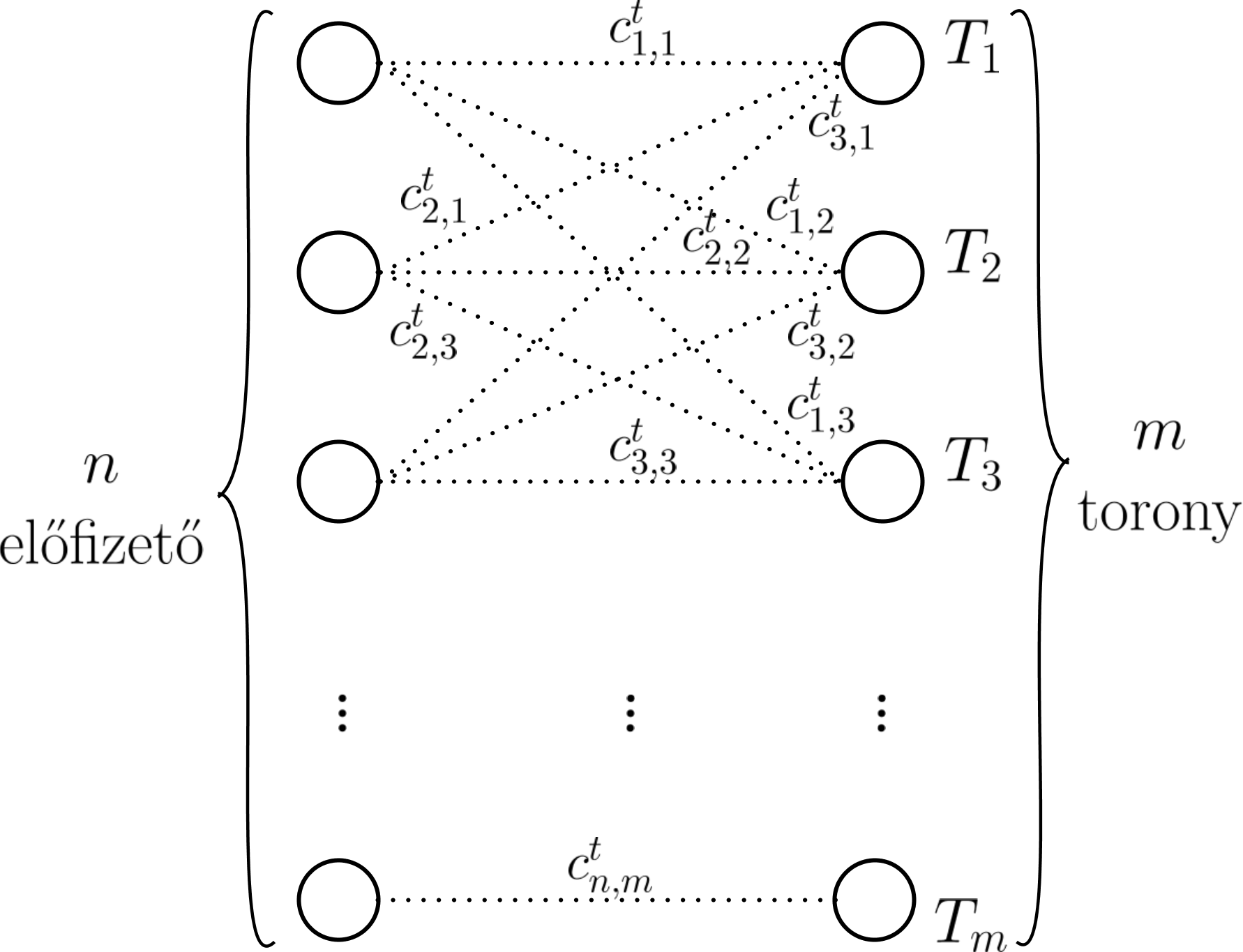 |
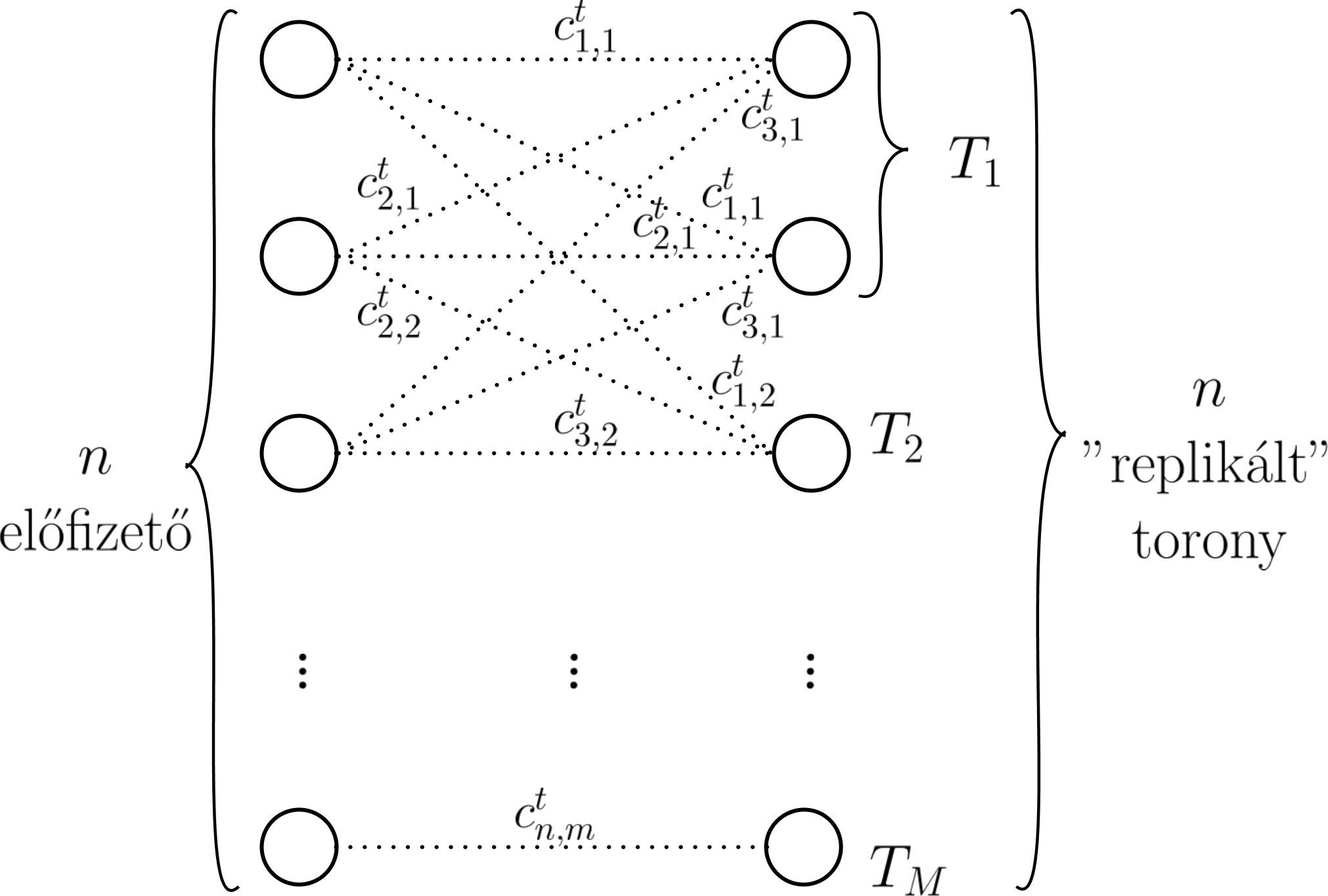 |
A támadás menete a következő: A t=1 időpontban tetszőlegesen kitöltjük az \mathbf{Y}^1 mátrixot azokkal a feltételekkel, hogy (1) Y_{i,j}^1 \in \{0,1\}, (2) \sum_{i=1}^n Y_{i,j}^1 = p_{j}^1, és (3) \sum_{j=1}^m Y_{i,j}^1 = 1. Ezek után alkalmazzuk a fenti optimalizációs eljárást, és rekonstruáljuk \mathbf{Y}^t-t minden t>1 időpontra egymás után egy napon belül, majd ezt az eljárást megismételjük minden napra külön-külön. A kérdés már csak az, hogyan kell a c_{i,j}^t költség-értékeket beállítani? Az alábbiakban látni fogjuk, hogy ennek beállítása napszaktól függ: mivel nappal az előfizetők másként mozognak mint éjszaka, ezért $c_{i,j}^t$ értéke ennek megfelelően különböző a nappali és éjszakai időszakokban.
Éjszakák és nappalok
Éjszaka az emberek többsége otthon van, és nem mozog; ahogy a szerzők is megmutatták, az előfizetők több mint 60%-a csak egyetlen tornyot, míg 20%-a csak két különböző tornyot látogat meg az éjszaka folyamán. Sőt (nem meglepő módon) az emberek 90%-ának ez egyben megegyezik a leggyakrabban meglátogatott (otthonukhoz közel levő) toronnyal.
Ennek megfelelően feltételezhető, hogy éjszaka minden torony költsége arányos a legutolsó időpontban meglátogatott toronytól mért távolságával. Pontosabban legyen egy T_j torony földrajzi pozíciója q_j minden 1 \leq j \leq m-re. Ha egy i előfizető a t-1 időpontban a T_j tornyot látogatta meg (vagyis Y_{i,j}^{t-1} = 1), akkor c_{i,k}^t = \text{distance}(q_j, q_k) minden 1 \leq k \leq m-re.
Nappal viszont az emberek gyakran mozognak, ezért a költségek máshogy alakulnak. Nappal egy előfizető által meglátogatott torony jól becsülhető az utolsó időpontban meglátogatott toronyból, valamint az előfizető mozgási sebességéből. Pontosabban ha egy i előfizető a (t-2) időpontban a T_{s} tornyot, t-1-ben pedig a T_{j} tornyot látogatta meg (vagyis Y_{i,s}^{t-2} = 1, Y_{i,j}^{t-1} = 1), akkor c_{i,k}^t = \text{distance}(q_k, q_j + (q_j – q_s)) minden 1 \leq k \leq m-re.
Rekordok összerendelése egymást követő napokon
Egy megoldás lehet ha a \mathbf{Y}^t-t a fenti módszerrel rekonstruáljuk tetszőleges t időpontig figyelembe véve a nappalok és éjszakák közötti különbségeket.
A gyakorlatban viszont a rekordok regularitása és egyedisége miatt jobb eredményt kapunk, ha az egész folyamatot minden nap újrakezdjük, és az egyes napokat egymástól függetlenül rekonstruáljuk, végül az azonos előfizetőhöz tartozó rekordokat összkapcsoljuk az egyes napok között a következő módszerrel.
Vegyünk két rekonstruált rekordot két egymást követő nap. Ha a két rekord ugyanahhoz az előfizetőhöz tartozik, akkor a két rekord relatív (egymáshoz viszonyított) információ tartalma kicsi, mivel mindkét rekordban hasonló gyakorisággal látogatták meg ugyanazon tornyokat (regularitás miatt). Vagyis ha az egyik nap ismerjük az előfizető rekordját, akkor a következő napi rekordja már nem hordoz túl sok információt az előző napihoz képest. Precízebben,
ha kiszámoljuk a két rekord entrópiájának átlagát, illetve a két rekord összefűzéséből kapott összesített rekord entrópiáját, a két értéknek hasonlónak kell lenniük ha a rekordok is hasonlóak, és a kettő közötti különbséget nevezzük információs nyereségnek (information gain). Tehát ha két rekord hasonló, akkor a kettő relatív információs nyeresége 0-hoz közeli, máskülönben 1-hez közeli.
Miután két egymást követő nap rekonstruáltuk az összes rekordot (ezeket az egy naphoz tartozó \mathbf{Y}^t mátrixok azonos sorszámú sorainak az összefűzéséből kapjuk), akkor kiszámoljuk az összes így kapott rekord és a következő nap hasonló módon kapott rekordjai közötti információs nyereséget. A feladat ezután a különböző napok rekordjainak összepárosítása úgy, hogy a kapott párosítások összköltsége (a páronkénti információs nyereségek összege) minimális legyen. Ez szintén a fentihez hasonló összerendelési probléma, és szintén megoldható a magyar módszerrel. Ez az összerendelés azért fog működni, mert minden rekord egyedi, és az azonos előfizetőhőz tartozó rekordok minden nap nagyon hasonlóak.
Eredmények
A szerzők kipróbálták a fenti támadást két adatbázison. Az első (Operator) 100 000 előfizető CDR adatát tartalmazta, vagyis minden előfizetőhöz rögzítették az időpontot és tornyot amikor az illető a mobilhálózatot használta 1 hetes időtartományban. A második (App) adatbázis 15 000 felhasználó tornyát rögzítette 2 hetes időtartományban, amikor azok elindítottak egy adott alkalmazást. Mindkét adatbázis ugyanabból a városból származik, amely 8000 toronnyal van lefedve. Mindkét esetben kiszámolták, hogy csakis \mathbf{P}^t-t felhasználva átlagosan egy előfizető hány torony-látogatását tudják helyesen rekonstruálni (vagyis a látogatás tornyát és idejét). Az eredményt az alábbi ábra mutatja.
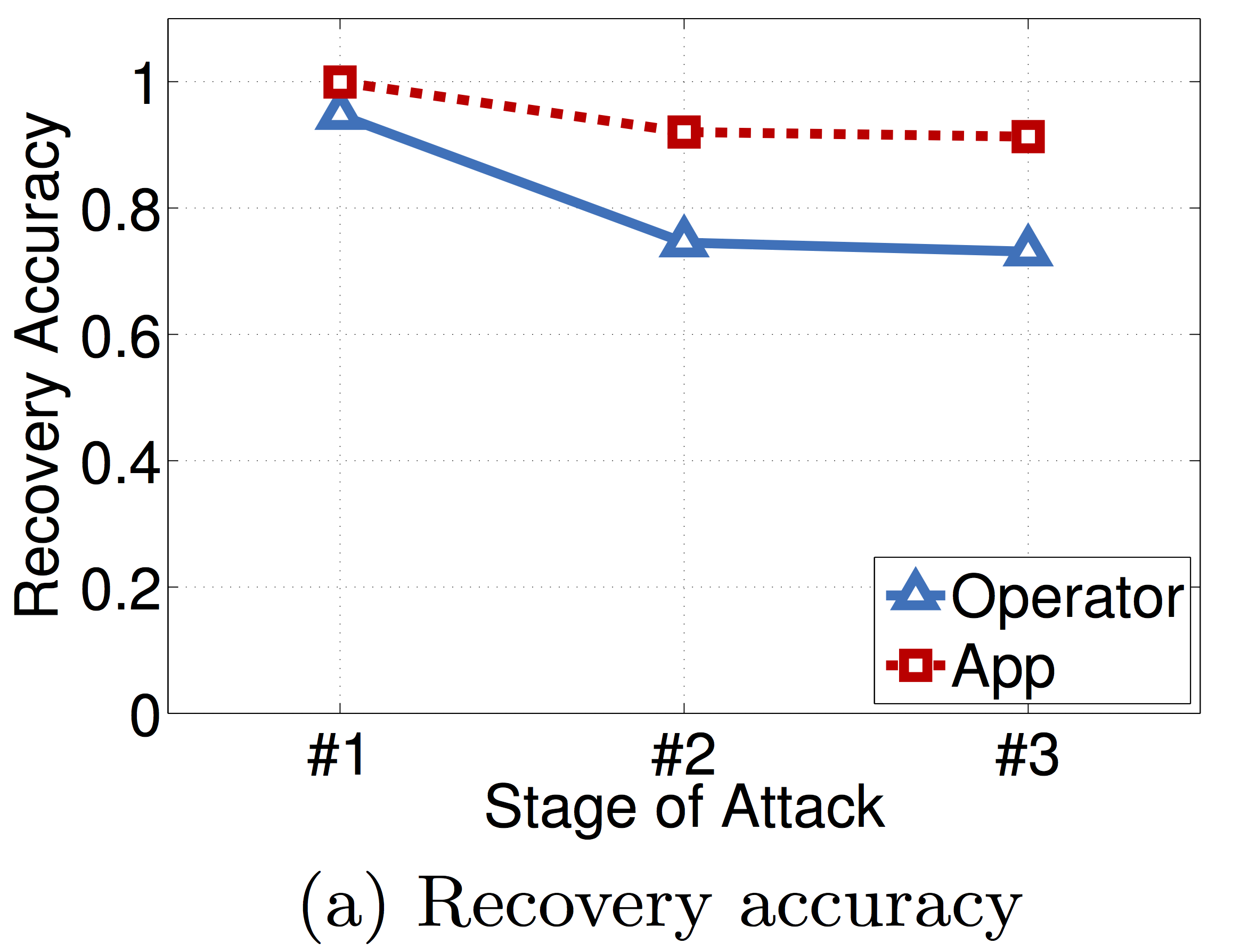
Stage1/Stage2 jelenti az éjszakai időtartománynak megfelelő rekordrészek átlagos rekonstrukciós pontosságát, míg Stage3 az egész támadás átlagos pontosságát a rekordrészek összefűzése után. Látható, hogy átlagosan egy rekord 91%-át sikeresen rekonstruálták az App adatbázisból számolt statisztikai adatból, míg ez az érték 73% az Operator adatbázis esetén.
Mivel a rekonstrukciós pontosság magas és 4-5 rekonstruált toronylátogatás már 95%-os eséllyel egyedi egy előfizetőre nézve akár egy több milliós populációban, ezért a támadás sikervalószínűsége nagy. Sőt,
az előfizetők azonosításához szükséges 4-5 torony meghatározása könnyű publikus Facebook/Instagram/Twitter profilokat felhasználva. Mivel más háttérinformáció nem szükséges az előfizetőkről, a támadás plauzibilis is, vagyis az egyes tornyok látogatottsága az idő függvényében (\mathbf{P}^t) jó eséllyel személyes adatnak minősül a GDPR 4. cikke szerint is.
Konklúzió
Láthattuk, hogy statisztikai adatok azért minősülhetnek személyesnek, mert azokból az eredeti adatbázis rekordjainak nagy része gyakran helyreállítható. Ennek oka, hogy ha túl sok aggregált adatot adunk ki (pl. túl sok lekérdezést válaszolunk meg), akkor még ha egyenként nem is, de a válaszok együttvéve jelentős információt szivárogtatnak ki az adatbázis egyes rekordjairól. Azt is láthattuk, hogy a lekérdezések tiltása az eredményeik nagysága alapján (vagyis amikor túl kicsi eredményű lekérdezést nem válaszolunk meg) nem feltétlen nyújt védelmet az ilyen támadások ellen, mivel nem a lekérdezések értéke, hanem a megválaszolt különböző lekérdezések száma és a támadó háttértudása (pl. az adat jellemzői) számítanak.
Hogyan védekezhetünk? Alapvetően két megközelítés létezik:
- A lekérdezések auditálása (query auditing), vagyis annak ellenőrzése, hogy a megválaszolandó lekérdezések lehetővé teszik-e valamely rekord rekonstruálását (pl. a fentihez hasonló egyenletrendszer megoldásával). A megközelítés feltevése, hogy ismerjük a legjobb rekonstrukciós eljárást, és megnézzük, hogy az sikeres lenne-e ha megválaszolnánk a lekérdezéseket. Ez a GDPR-nak meg is felelhet, ha a rekonstrukció sikervalószínűsége nem túl magas és a rekonstrukciós eljárás “plauzibilis” a gyakorlatban (vagyis a potenciális támadók valóban nem fognak ennél jobbat használni).
Viszont az eddigiek tükrében két problémával érdemes számolni:
(1) A legtöbb auditálási eljárás feltételezi, hogy a támadónak nincs háttértudása a rekordokról. Ahogy fent láttuk, ez a gyakorlatban nem mindig igaz; pl. ismerhet néhány rekordot, vagy ismeretlen rekordokról lehet részleges tudása (ld. predikálhatóság, regularitás, egyediség). Ez a támadót segítheti, hiszen például a vártnál kevesebb lekérdezésből képes lehet az ismeretlen rekordokat visszaállítani. Ugyanakkor ezt a háttértudást a gyakorlatban szinte lehetetlen modellezni az egyének magukról vagy másokról megosztott információk sokasága miatt.
(2) Ha mégis sikerül detektálni a problémás lekérdezést (ami egyébként nehéz), akkor dönthetünk úgy, hogy azt nem válaszoljuk meg. Ekkor viszont nem adunk ki adott esetben értékes adatot, aminél van jobb megoldás is (ld. alább). - A lekérdezések eredményeinek zajosítása/randomizálása (query perturbation), vagyis mielőtt kiadnánk a lekérdezések eredményét, hozzáadunk azokhoz egy zérus várható értékű \lambda szórású zajt. Ha \lambda (és így a zaj várható nagysága) kisebb, az érték pontosabb, viszont a fenti támadások nagyobb eséllyel működhetnek. Ha \lambda nagyobb, akkor az adat jobban védett a nagyobb zaj miatt, és a fenti támadások kisebb eséllyel működnek (viszont a kiadott adat is pontatlanabb).
Ez egy alapvető kompromisszum a statisztikai adatok hasznossága (pontossága) és a személyes adatok védelme között az informatikában.
A zaj nagyságának megfelelő beállítása nem könnyű és szakértelmet igényel, ami a manapság egyre szélesebb körben alkalmazott Differential privacy-nek is az alapja. A gyakorlatban ezt a megközelítést alkalmazta már a Google, majd később az Apple és Uber is.
A CrySyS laborban lekérdezések auditálásával illetve lekérdezések eredményeinek torzításával is aktívan foglalkozunk.